
인간은 참 잘한다 발견 패턴또는 사람들이 인식할 수 있는 기능을 반복합니다. 예를 들어, 고대 폴리네시아인들은 다음과 같은 방법으로 태평양을 건너 항해했습니다. 다양한 패턴 인식성단부터 바다 너울의 방향과 크기와 같은 더 정확한 것까지.
아주 최근, 나 같은 수학자 그들은 특정 유형의 패턴이 없는 대규모 개체 그룹을 연구하기 시작했습니다. 클러스터 어딘가에서 특정 패턴이 나타나기 전에 클러스터는 얼마나 커질 수 있습니까? 이러한 시나리오를 이해하면 실제 세계에 큰 영향을 미칠 수 있습니다. 예를 들어 인터넷을 중단시킬 수 있는 서버 오류의 최소 횟수는 얼마입니까?
수학자의 연구 조던 엘렌버그 위스콘신 대학교 연구진은 구글 딥마인드 이 문제에 대한 새로운 접근 방식이 제안되었습니다. 그들의 일 인공지능을 이용해 찾아낸다. 대규모 클러스터에는 특정 패턴이 없으므로 일부 최악의 시나리오를 이해하는 데 도움이 될 수 있습니다.
카드 게임 세트의 패턴
꾸미지 않은 덱의 아이디어는 인기 있는 카드 게임으로 설명할 수 있습니다. 그는 그룹에 전화를 걸었습니다.. 이 게임에서 플레이어는 12장의 카드를 앞면이 보이도록 놓습니다. 각 카드에는 서로 다른 간단한 이미지가 포함되어 있습니다. 숫자, 색상, 모양 및 음영이 다양합니다. 이러한 네 가지 기능은 각각 세 가지 값 중 하나를 가질 수 있습니다.
플레이어는 각 카드의 각 기능이 동일하거나 다른 세 개의 카드로 구성된 그룹인 “수트”를 찾기 위해 경쟁합니다. 예를 들어, 고체 빨간색 다이아몬드 1개, 고체 녹색 다이아몬드 2개, 고체 보라색 다이아몬드 3개가 포함된 카드는 모양을 구성합니다. 세 카드는 모두 서로 다른 숫자(1, 2, 3), 동일한 음영(단색) 및 서로 다른 색상(빨간색)을 갖습니다. , 녹색, 보라색)과 같은 모양(다이아몬드)입니다.
일반적으로 그룹을 찾는 것이 가능하지만 항상 그런 것은 아닙니다. 두 플레이어 모두 테이블에서 12장의 카드 세트를 찾을 수 없으면 3장의 카드를 더 뒤집습니다. 하지만 여전히 이 15장의 카드 조합을 찾을 수 없습니다. 플레이어는 누군가 조합을 발견할 때까지 한 번에 세 개씩 카드를 계속 뒤집습니다.
그렇다면 덱을 구성하지 않고 배치할 수 있는 최대 카드 수는 몇 장입니까?
1971년 수학자 주세페 펠레그리노(Giuseppe Pellegrino)는 다음과 같은 사실을 보여주었습니다. 무늬가 없는 가장 큰 카드 세트는 20장입니다.. 하지만 무작위로 20장의 카드를 선택하면 “No Combo”만 발생합니다. 1000억분의 1 정도. 이러한 “미확인” 그룹을 찾는 것은 해결하기 매우 어려운 문제입니다.
인공지능을 활용해 '그룹 없음' 찾기
덱 없이 가장 작은 카드 세트를 찾으려면 원칙적으로 81개 카드 덱에서 선택한 가능한 모든 카드 조합에 대해 철저한 검색을 수행할 수 있습니다. 그러나 10분 안에 수많은 가능성이 있습니다.24 (이것은 “1” 뒤에 0이 24개 오는 형태입니다.) 예를 들어, 카드 기능의 수를 4개에서 8개로 늘리면 문제의 복잡성이 “정의되지 않은” 조합을 철저하게 검색하는 모든 컴퓨터를 압도하게 됩니다.
수학자들은 이와 같이 계산적으로 어려운 문제에 대해 생각하는 것을 좋아합니다. 이러한 복잡한 문제는 올바른 방법으로 처리하면 해결할 수 있습니다.
최상의 시나리오를 찾는 것이 더 쉽습니다. 여기서는 덱에 포함될 수 있는 최소 카드 수를 의미합니다. 그러나 나쁜 시나리오를 해결할 수 있는 몇 가지 잘 알려진 전략이 있었습니다. 여기서는 덱이 없는 큰 카드 덱을 의미했습니다.
Ellenberg와 그의 협력자들은 대규모 언어 모델(LLM)이라고 불리는 일종의 인공 지능을 사용하여 나쁜 시나리오를 처리했습니다. 연구자들은 먼저 아무것도 포함하지 않은 많은 세트의 몇 가지 예를 생성하는 컴퓨터 프로그램을 작성했습니다. 이러한 덱에는 일반적으로 4개 이상의 기능을 포함하는 “카드”가 포함되어 있습니다.
그런 다음 이러한 프로그램을 LLM에 제공했는데, LLM은 여러 유사한 프로그램을 작성하는 방법을 빠르게 배우고 가장 큰 무료 그룹이 프로세스를 다시 거치게 하는 프로그램을 선택하는 방법을 배웠습니다. 가장 성공적인 프로그램을 반복적으로 조정하여 이 프로세스를 반복하면 클러스터가 없는 더 큰 클러스터를 찾을 수 있습니다.
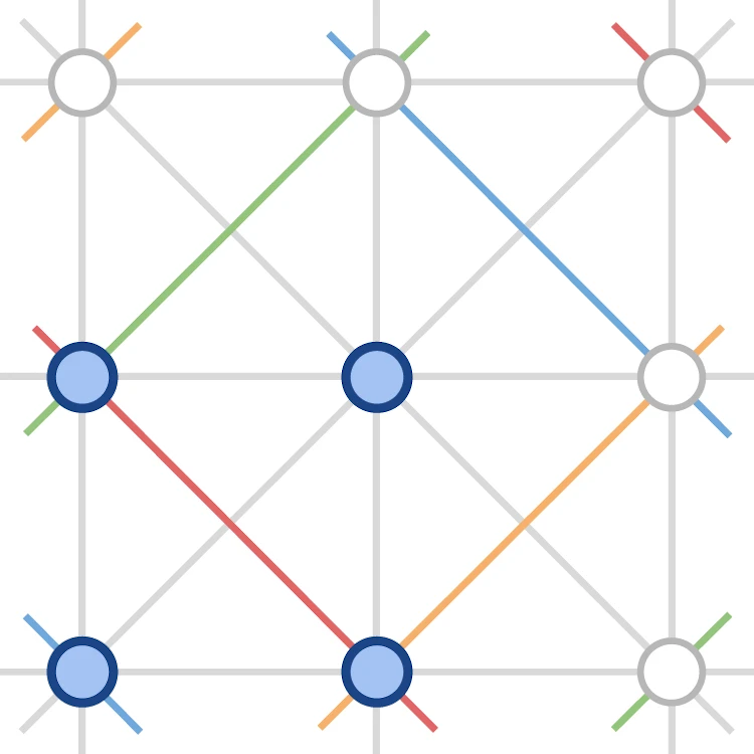
Romera Peredes 등/Nature, CC BY-SA
이 방법을 사용하면 사람들이 불규칙한 그룹을 탐색할 수 있습니다. 이 경우에는 슈트가 포함되지 않은 카드 모음 – 완전히 새로운 방식으로요. 연구자들이 절대적으로 최악의 시나리오를 찾을 것이라고 보장하지는 않지만 무작위 생성으로 인해 발생하는 것보다 훨씬 더 나쁜 시나리오를 찾을 것입니다.
그들의 연구는 연구원들이 사건이 어떻게 재앙적인 실패로 이어지는 방식으로 정렬되는지 이해하는 데 도움이 될 수 있습니다.
예를 들어, 특정 변전소를 파괴하는 악의적인 공격자에게 전기 네트워크는 얼마나 취약합니까? 잘못된 변전소 세트가 연결된 네트워크를 형성하지 않는 변전소 세트라고 가정해 보십시오. 현재 최악의 시나리오는 함께 추가해도 여전히 연결된 네트워크를 생성하지 못하는 변전소가 너무 많다는 것입니다. 이 그룹에서 제외된 변전소의 수는 악의적인 행위자가 의도적으로 네트워크 연결을 끊기 위해 파괴해야 하는 가장 작은 수입니다.
Ellenberg와 그의 협력자들의 연구는 AI가 매우 강력한 도구가 될 수 있다는 또 다른 방법을 보여줍니다. 그러나 적어도 현재로서는 매우 복잡한 문제를 해결하려면 여전히 인간의 독창성이 필요합니다.